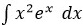| ATIVIDADE 3 – CÁLCULO DIFERENCIAL E INTEGRAL I – 54_2024 | |
| Período: | 21/10/2024 08:00 a 24/11/2024 23:59 (Horário de Brasília) |
| Status: | ABERTO |
| Nota máxima: | 1,00 |
| Gabarito: | Gabarito será liberado no dia 25/11/2024 00:00 (Horário de Brasília) |
| Nota obtida: | |
| 1ª QUESTÃO | |||||||||||
|
No cálculo integral há basicamente duas técnicas de integração: Integração por Substituição e Integração por Partes. A base da dedução deste último método vem da Regra do Produto vista na diferenciação.
Fonte: Dicas de Cálculo. Integração por Partes. Disponível em: <https://www.dicasdecalculo.com.br/conteudos/integrais/integracao-por-partes/>. Acesso em 17 mar 2023.
Utilizando a técnica de integração por partes, encontre
|
|||||||||||
| ALTERNATIVAS | |||||||||||
|
|||||||||||
| 2ª QUESTÃO | |||||||||||
|
Nem sempre devemos, ou podemos, calcular as derivadas diretamente a partir da definição, usando o limite da razão incremental, pois este método, além de ser repetitivo para certas funções como as lineares e polinomiais, só é prático para funções muito particulares e simples. Temos algumas regras de derivação que permitem obter derivadas de funções de uma forma mais fácil e rápida. Por exemplo, na divisão de funções, quando o denominador g(x) é não nulo, a derivada pode ser obtido como:
Neste caso, a ordem das funções f e g, não pode ser mudada. Disponível em: http://www.uel.br/projetos/matessencial/superior/calculo/derivada2.html. Acesso em: Agosto. 2024 (adaptado). Sobre as regras para obter a derivada de uma função, se derivarmos a função f(x) = (100x+300) / (x+10) e calcular a sua derivada no valor zero, obtemos um valor de: |
|||||||||||
| ALTERNATIVAS | |||||||||||
|
|||||||||||
| 3ª QUESTÃO | |||||||||||
|
O processo de encontrar uma primitiva para uma integral é bem mais difícil que o de calcular uma derivada. Existem vários métodos importantes que nos ajudam nesse objetivo, um deles é o método da mudança de variáveis ou substituição. Nesse sentido, utilize o método de integração por substituição para resolver a integral
|
|||||||||||
| ALTERNATIVAS | |||||||||||
|
|||||||||||
| 4ª QUESTÃO | |||||||||||
|
Algumas regras para derivadas de funções podem ser representadas por expressões com termos simples, o que ocorre com funções conhecidas, mas tais regras não se aplicam a funções mais complexas. Por exemplo, f(x)=(4x+1)100 pois, é quase impossível derivar um produto com 101 termos usando regras usuais e derivação de funções. Mas, podemos expressar esta função como a composta de duas funções mais simples, motivo pelo qual, aprende-se a derivar qualquer função formada pela composição de funções com derivadas conhecidas. Por exemplo, a seguir é apresentado a Regra da Cadeia, que permite derivar uma função composta. Regra da cadeia: Sejam f e g funções diferenciáveis e a função composta definida por h(x) = f(g(x)). Se u = g(x) é derivável no ponto x e se y = f(u) é derivável no ponto u = g(x), então a função composta h é derivável no ponto x e a sua derivada é dada por:
Fonte: Disponível em: http://www.uel.br/projetos/matessencial/superior/calculo/derivada2.html. Acesso em: Agosto. 2024. (adaptado). Observado o texto acima, referente ao procedimento de se derivar uma função composta, observe a função f(x) = (2x+3)5. Derivando a função f(x) e calculando a derivada no valor 1, obtem-se um valor de: |
|||||||||||
| ALTERNATIVAS | |||||||||||
|
|||||||||||
| 5ª QUESTÃO | |||||||||||
|
Você precisa determinar a área de um terreno irregular para estimar o investimento necessário para aquisição do mesmo. Avaliando o terreno, você percebeu que poderia representar os limites do terreno por duas funções sendo f(x) = 5x – x2 e g(x) = x. Determine o custo deste terreno limitado pelas duas funções, sabendo que ele vale R$150,00/m2. Arredonde a área final para duas casas decimais e assinale a alternativa correta.
|
|||||||||||
| ALTERNATIVAS | |||||||||||
|
|||||||||||
| 6ª QUESTÃO | |||||||||||
Determine se a integral converge ou diverge, e assinale a alternativa correta: |
|||||||||||
| ALTERNATIVAS | |||||||||||
|
|||||||||||
| 7ª QUESTÃO | |||||||||||
| Assinale a alternativa que contenha a correta solução para o trabalho realizado quando uma força de x3 + xN age sobre uma partícula, movendo-se de x = 2 até x = 4: |
|||||||||||
| ALTERNATIVAS | |||||||||||
|
|||||||||||
| 8ª QUESTÃO | |||||||||||
. |
|||||||||||
| ALTERNATIVAS | |||||||||||
|
|||||||||||
| 9ª QUESTÃO | |||||||||||
|
O setor de autopeças representa uma cadeia produtiva fundamental para o complexo automotivo, sendo responsável por parte significativa do desenvolvimento tecnológico, tanto a partir de encomendas das montadoras quanto a partir de inovações e aprimoramentos autônomos. Além disso, segundo o Instituto Brasileiro de Geografia e Estatística (IBGE), a indústria de autopeças emprega 331 mil trabalhadores no Brasil, sem contar o contingente de mão de obra alocado no setor de serviços (atacadistas, varejistas, assistência técnica etc.), em 3.077 empresas, das quais 1.824 com cinco ou mais empregados. A indústria de autopeças obteve um faturamento de R$ 76,8 bilhões em 2014.
Fonte: Disponível em: https://web.bndes.gov.br/bib/jspui/bitstream/1408/9555/1/BNDES%20Setotrial%2042%20Panorama%20da%20ind%C3%BAstria%20de%20autope%C3%A7as%20no%20Brasil_P_P.pdf. Acesso em: Agosto. 2024. (adaptado). Com relação a produção e vendas de peças automotivas, uma empresa, ao vender um determinado tipo de peça, tem a variação instantânea, ou seja, a derivada da função receita dada por R ‘ (q) = 3.q2, e a derivada da função custo, dada por C ‘ (q) = 27, onde q, representa a quantidade de peças fabricadas e vendidas. Sabendo que a função lucro pode ser obtida pela diferença entre a função receita e a função custo, no que representa qual será o lucro da empresa, quando for vendido a quantidade de peças entre 6 e 10 peças, assinale a alternativa correta: |
|||||||||||
| ALTERNATIVAS | |||||||||||
|
|||||||||||
| 10ª QUESTÃO | |||||||||||
|
Para encontrar a derivada parcial de uma função f(x,y) com relação a x, basta olhar y como uma constante e diferenciar f(x,y) com relação a x. Sabendo disso, encontre fx(2,2) da função f(x,y) = x2+ xy2 – 2y, e assinale a alternativa correta.
|
|||||||||||
| ALTERNATIVAS | |||||||||||
|
|||||||||||